

Therefore the viscous work term must be zero. In other words, we can lump all the viscous work terms together into one term, and call it. So here, even though is not zero along the blades themselves, we can avoid evaluating the integral since we include it in, which is usually either a given or an unknown in the problem. around the whole thing! We simply include all of the viscous and pressure work terms on these blades as part of. In this case, if the control surface is taken along the walls of the blades. For example, consider the blades of pumps or turbines

For flow along a stationary solid wall, it is the same - there is a force (per unit area) which is, but no motion. My teacher pushed on the wall with all his might and said, "How much work am I doing?" Answer: None! Work = Force x Distance. there is a shear stress acting on the fluid.) But, (no slip condition at a wall!), i.e.Īnalogy - Think back to high school physics class when you first learned about the concept of work. Here are some examples:Īlong this wall, since there is friction acting, (i.e. But for most control volumes that we will deal with, it turns out to be zero.
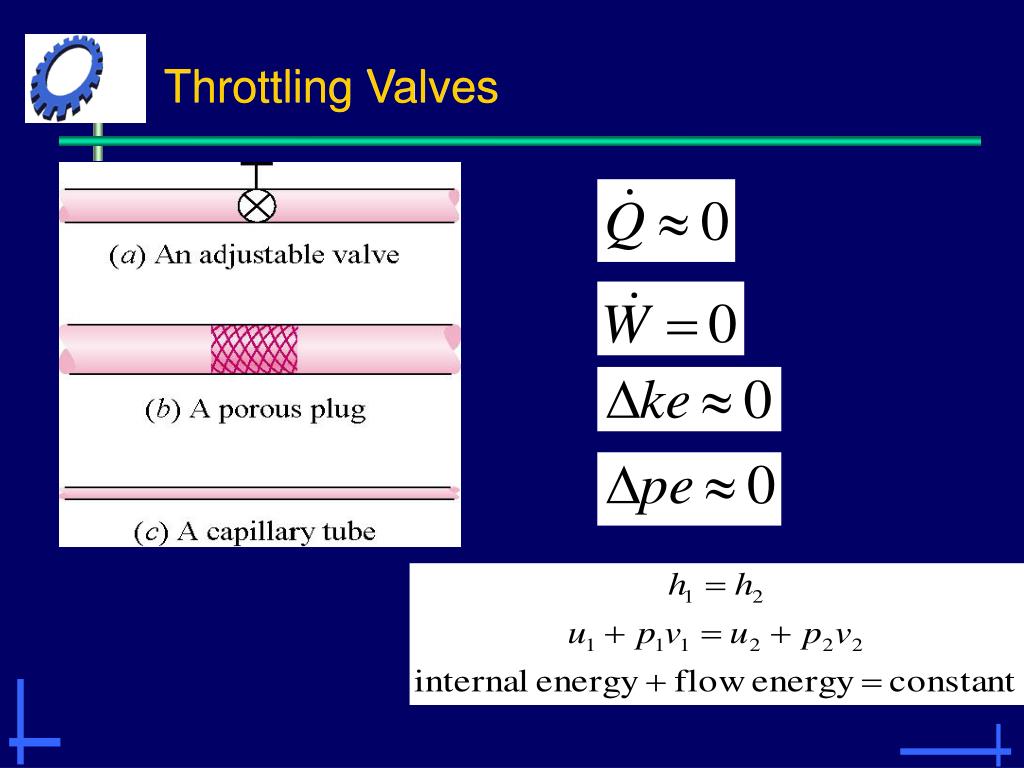
, which is a complicated and ugly term to try to evaluate. A similar thing happens in the energy equation. Fortunately, we could either eliminate it by proper choice of C.V. Cases where = 0: Recall when we talked about the momentum equation, we had a term that was hard to evaluate.I.e., viscous work is being done by the moving wall on the fluid. On the top surface of the control volume,, so, (The top wall is moving, but the bottom wall is fixed.) a case in which, consider the control volume sketched below in which part of the control surface lies along a moving wall with friction. As an example of a case where this is not the case, i.e. This is The general equation of conservation of energy for a fixed control volume.įor a lot of problems. Plugging these into the above equation yields Plug all of these back into the energy equation, but put the pressure work term on the right hand side:īut, and from the definition of enthalpy (per unit mass).If we define vector as the resultant shear stress acting on the C.S., it turns out that. Rate of viscous work, = rate of work done by viscous stresses at the control surface.Rate of Pressure Work, = rate of work done by pressure forces at the control surface.Note: is positive for a turbine (work done by the fluid), and is negative for a fan (work done on the fluid). a turbine (extracts energy from a flow) : The turbine takes energy from the fluid and converts it into rotation of the shaft. Rate of Shaft Work, = rate of work done by the fluid on a shaft protruding outside the C.V.Į.g.Let's look at each of these terms individually: Has dimensions of = Power (so these are actually power terms). , where: = rate of shaft work, = rate of pressure work, = rate of viscous work. Generally, what is done is to split the work term up into 3 parts:.

= kinetic energy per unit mass, gz = potential energy per unit mass. Where e = total energy of the fluid per unit mass,, = internal energy per unit mass, Thus, the right side of the above equation can be called the General Integral Equation for Conservation of Energy in a Control Volume, The left side of the above equation applies to the system, and the right side corresponds to the control volume. In the Reynolds Transport Theorem (R.T.T.), let.Where = rate of change of total energy of the system, = rate of heat added to the system, = rate of work done by the system Recall, the First Law of Thermodynamics:.


 0 kommentar(er)
0 kommentar(er)
